Activités sur la reconnaissance et la décomposition des nombres <10

​

Niveau : cycle 2

Compétences :
– Procédures de dénombrement (décompositions/recompositions additives)
– Utiliser diverses représentations des nombres

Matériel :

Source : le matériel est inspiré de https://www.mathcoachscorner.com/2013/07/using-number-bracelets-to-develop-number-sense/ mais les activités proposées ci-dessous ne s’inspirent pas de ce site excepté les combinaisons et la complétion d’additions.

Découverte du matériel

Découverte du matériel : le matériel est proposé aux élèves, autant de jeux de 10 bracelets que d’enfants. Proposer aux élèves de ranger les bracelets sans davantage de consigne. Cela permet aux élèves de prendre contact avec le matériel, et d’en observer les particularités.

L’enseignant doit s’assurer que les attributs suivants ont été observés :

• Le nombre indiqué sur l’étiquette correspond au nombre de perles
• Un jeu est composé de 10 éléments (bracelets) représentant les nombres de 1 à 10
• Il y a plusieurs jeux de 10 bracelets (si plusieurs jeux sont proposés)

Aide possible : après répartition d’un jeu par élève, proposer aux élèves de ranger leur collection du plus petit au plus grand, en leur proposant par exemple les 2 premiers blacelets rangés.

Reconnaître les nombres de 1 à 10

Objectif.s
– connaître et reconnaître les nombres de 1 à 10

Disposer les bracelets dans l’ordre. Faire fermer les yeux aux élèves, puis enlever un bracelet. Les élèves doivent retrouver quel bracelet a été enlevé. Ensuite, proposer la même activité avec les bracelets dans le désordre.

Pré-requis
– connaître la comptine jusque 10

Aides
– disposer les chiffres dans l’ordre constitue une première aide.
– proposer une file numérique jusque 10 en aide individuelle.

Variables didactiques
– enlever un seul bracelet
– enlever deux bracelets
– demander combien de bracelets ont été enlevés
– changer l’ordre des bracelets, mais les laisser en ligne
– disposer les bracelet de façon à ce qu’ils ne soient pas en ligne

Progression
– proposer les bracelets dans l’ordre
– proposer les bracelets dans le désordre
– supprimer les aides (file numérique individuelle)

Indicateurs de réussite
– l’élève sait associer le nombre au bracelet
– l’élève sait retrouve le bracelet qui a été enlevé

Décomposition de nombres

Objectif.s
– découvrir qu’un nombre est une composition de nombres
– décomposer les nombres <10
– aller de la manipulation à l’abstraction et l’écriture chiffrée

Proposer un seul bracelet aux élèves, par exemple le 4. Faire décompter les 4 perles et le mettre en rapport avec l’étiquette.
Demander aux élèves de séparer les perles en 2 groupes et de compter compter combien il y a de perle dans chacun des groupes, puis de trouver toutes les façons de faire 2 groupes.
Le travail peut d’emblée être dessinée, et pourra servir de trace visuelle des décompositions trouvées.

​

Pré-requis
– connaître les chiffres de 1 à 10
– connaître la comptine numérique jusque 10

Aides
– dire que l’on peut commencer par mettre une perle de côté et compter le reste (pour amorcer)
– annoncer d’emblée qu’il y a en tout 2 façons de faire des groupes
– proposer directement la séparation en 2 groupes, et ne demander à l’élève que de dénombrer
– utiliser des expressions imagées, « couper en deux » etc.

Variables didactiques
– décomposer des bracelets 4, 5 uniquement, car il n’y a qu’une seule décomposition de 2 et 3, et au delà de 5 la tâche devient plus grande.
– si l’élève décompose facilement avec le matériel, lui proposer de dessiner ses recherches
– si l’élève a trouvé les décompositions et a du les dénombrer, il peut associer l’écriture chiffrée en dessous de ses dessins
– si l’élève est capable d’abstraction et connaît bien les chiffres de 1 à 10, il peut écrire les décompositions en écriture chiffrée

Progression
– séparer les perles en 2 groupes sur le matériel
– trouver toutes les décompositions
– dénombrer les 2 groupes en repartant de 1 à chaque groupe
– dessiner les bracelets décomposés
– schématiser les décompositions (libre)
– schématiser et associer l’écriture chiffrée
– utiliser l’écriture chiffrée uniquement pour décrire les décompositions

Indicateurs de réussite
– l’élève essaie de trouver une décomposition supplémentaire
– l’élève compte chaque groupe en repartant de 1
– l’élève sait lorsqu’il a trouvé toutes les décompositions

 

Mise en relation de la décomposition visuelle avec l’addition

Objectif.s
– faire une décomposition additive
– remarquer le caractère associatif de l’addition

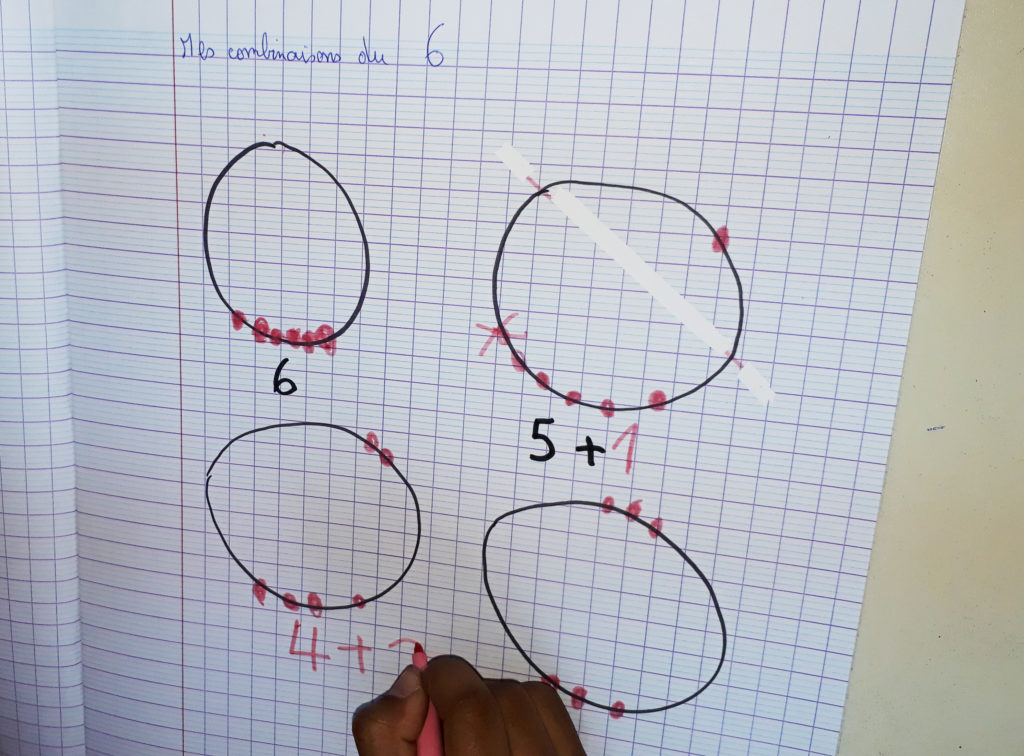
Faire écrire aux élèves les 2 nombres trouvés dans chaque groupe. Faire verbaliser la relation qui est unie, et le formaliser mathématiquement par un +.
Les élèves doivent écrire toutes les additions correspondantes aux décompositions qu’ils ont identifiées.

Progression
– décomposer tous les bracelets jusque 10

Indicateurs de réussite
– trouver toutes les décompositions des nombres <10
– remarquer le caractère commutatif de l’addition (ne pas écrire 2 fois la même décomposition en réussissant à l’identifier comme identique)

Remarquer l’itération

1/ Faire préalablement ranger tous le bracelets de 4 à 10 dans l’ordre croissant.
2/ Demander aux élèves de mettre systématiquement 1 perle de côté dans chaque bracelet. Leur demander de nommer la décomposition correspondante et de l’écrire en dessous sur une étiquette.
3/ Leur faire lire toutes les étiquettes une par une et leur demander ce qu’ils remarquent. Les élèves doivent identifier qu’on ajoute 1 à chaque fois au nombre précédent. 4 c’est 3+1, 5 c’est 4+1.

Activité 1 : donner un nombre aux élèves et poser les questions suivantes :
« quel est le nombre qui vient juste avant ? »
ou « quel est le nombre qui vient juste après ? »
ou « quel est le suivant ? Le précédent ? »
ou « X et un, ça fait combien ? »

Exercice 2 : l’enseignant tape un certain nombre de fois dans ses mains. Les élèves doivent dire quel nombre vient juste après. Plutôt que de le dire oralement, ils peuvent aussi l’écrire sur une ardoise.

Décomposition en 3 nombres

1/ Travailler avec les bracelets 3, 4, 5 et 6.
2/ Demander aux élèves de faire 3 groupes de perles dans tous les bracelets.
3/ Leur demander d’écrire sur des étiquettes les additions correspondantes.
4/ Pour le bracelet 5, donner 1 autre étiquette et demander de trouver et d’écrire un autre partage. (1+2+2) (1+3+1)
5/ Pour le bracelet 6, donner 2 autres étiquettes et demander aux élèves de trouver 2 autres façons de partager en 3. (1+1+4) (1+2+3) (2+2+2)

Décomposition en 4 nombres

1/ Travailler avec les bracelets 4, 5 et 6 et 7.
2/ Procéder de la même façon que pour la décomposition en 3 nombres.
Bracelet 4 : (1+1+1+1)
Bracelet 5 : (1+1+1+2)
Bracelet 6 : (1+1+1+3) (1+1+2+2)
Bracelet 7 : (1+1+1+4) (1+1+2+3)

Complétion d’additions

A/ jeu
Tirer une carte nombre au hasard inférieur à 10. La poser sur la table visible des joueurs.
Donner à chaque joueur 1 ou plusieurs jetons jaunes ou bleus (inférieur au nombre carte).
Le maître possède tous les jetons verts. Chaque élève doit formuler une demande de jetons verts pour compléter sa collection jusqu’au nombre affiché sur la carte. Le maître lui donne et l’élève dénombre sa collection pour vérifier son total de jetons. Si c’est égal au nombre indiqué sur la carte, il gagne 1 lingot d’or.
L’élève qui a gagné sera celui qui aura le plus de lingots d’or (décompter en formulant untel en a 2 ou 3 de plus que untel, en les alignant par exemple).

Exemple : le maître pose une carte « 7 » sur la table. Il donne 3 jetons bleus à un élève, et 4 jetons jaunes à l’autre élève. Le premier élève doit demander 4 jetons verts au maître, et l’autre élève doit demander 3 jetons verts au maître. Les joueurs recomptent leur collection pour vérifier qu’ils ont bien 7 jetons en tout. S’ils ont gagné, ils reçoivent un lingot d’or qu’ils mettent de côté.

Variables didactiques / différentiation
– La carte nombre posée au milieu prend des représentations différentes du nombre (collection, mains, dés, abaques)
– Les élèves reçoivent une carte nombre de différente et de difficulté choisie

Progression
– On enlève les bracelets.
– On enlève les jetons : les élèves sont capables de compléter une addition.
– Le nombre de la carte est inférieur aux jetons donnés aux élèves : les élèves doivent donc penser à redonner des jetons et non plus en demander. Les élèves peuvent écrire l’opération sous forme de soustraction.

​

B/ Exercices
Réinvestir directement avec les bracelets sur des additions à compléter du type :
2 + … = 7, 3 + … = 4, 1 + … = 5

Activités de recomposition

1/ Donner le bracelet 4 aux élèves, et leur demander de trouver 2 bracelets pour faire 4 aussi. Ils proposeront 3+1. Leur faire vérifier en comptant sur les 2 bracelets. On peut mélanger les séries pour demander une autre façon de faire 4 (avec 2 bracelets de 2).
2/ Faire la même chose avec le bracelet 5, et aller jusqu’à 10.
3/ On peut prolonger l’activité en demandant de trouver 3 bracelets pour faire le chiffre demandé.
4/ En trace écrite, on peut demander à l’élève de dessiner le résultat de sa recherche sur 2 ou 3 bracelets, mais pas tous. Il devra en dessous de chaque recomposition écrire l’addition correspondante.

Quantités cachées

Proposer un bracelet aux élèves et cacher avec la main ou un cache une partie des perles. Demander aux élèves de trouver combien de perles sont cachées.

Objectif.s
– recomposer un nombre
– obliger l’élève à traiter effectivement 2 quantités
– aller vers l’abstraction et l’écriture chiffrée des décompositions

Stratégies possibles
– transposer les quantités sur les doigts et dénombrer la partie manquante
– sur-compter depuis la partie connue
– dessiner le bracelet et procéder à tâton
– faire un schéma autre que le bracelet
– sur-compter en dessinant des points ou des croix ou autre
– partir du chiffre d’arriver et barrer le nombre de perles visibles (dessin de bracelet ou schéma)

Aides
– coopération et échanges de stratégies entre pair
– schémas pré-imprimés des bracelets (perles à colorier ou bien faire un schéma)

​